-

-
خدمات آنالیز
- آنالیزهای طیف سنجی
- آنالیزهای میکروسکوپی
- آنالیزهای عنصری
- آنالیزهای الکتروشیمیایی
- آنالیزهای فیزیکی
- آنالیزهای کروماتوگرافی
- آنالیزهای شیمی تر و تیتراسیون
-
آنالیزهای سلولی، میکروبیولوژی و ژنتیک
-
روش های آماده سازی و تصویربرداری
- خدمات فریزدرایر (خشک کن انجمادی - Freeze dryer)
- میکروسکوپ کانفوکال (Confocal)
- خدمات تصویربرداری فلورسانت و رنگ آمیزی
-
آنالیزهای آنتی باکتریال
- آزمون آنتی باکتریال تعیین MIC و MBC
- آزمون آنتی باکتریال تعیین هاله عدم رشد (Disk diffusion)
- آزمون بررسی میزان آنتی باکتریال کالاهای نساجی (پارچه ها)
- بررسی خاصیت ضد قارچی پارچه ها
-
آنالیزهای مطالعه پروتئین ها و DNA
- Real Time PCR
- خدمات الکتروفورز افقی و عمودی
- خدمات SDS-PAGE
- آزمون برادفورد (سنجش کمی پروتئین ها)
- استخراج DNA از باکتری ها
- استخراج RNA
- سنتز cDNA
-
آنالیزهای سلولی برون تنی (In-Vitro)
- آزمون سمیت شناسی به روش MTT
- آزمون چرخه سلولی با فلوسایتومتری
- ارزیابی ROS با فلوسایتومتری
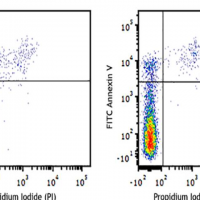
- ارزیابی سلول های آپاپتوتیک و نکروتیک به روش Annexin V-FITC/PI
- ارزیابی فعالیت کاسپازهای مختلف در رده سلولی
- اندازه گیری میزان نیتریک اکساید NO
- ارزیابی ظرفیت آنتی اکسیدانی به روش رادیکال DPPH
-
-
آنالیزهای متالورژی و خواص مکانیکی مواد
-
آنالیزهای غیر مخرب
- تست RT
- تست PT
- تست MT
-
آنالیزهای متالورژی و خوردگی
- خوردگی SCC
- خوردگی HIC
- آزمون متالوگرافی
- آزمون سالت اسپری
- عملیات حرارتی
- آسیاب گلوله ای سیاره ای
-
آزمون های خواص مکانیکی مواد
- آزمون کشش
- آزمون فشار
- آزمون خمش
- آزمون های سختی سنجی
- آزمون ضربه
- اسپین تست
-
-
آنالیزهای آب
-
آنالیزهای خاک
- تعیین مش بندی مواد با الک
- اندازه گیری کلراید در عصاره اشباع خاک
- اندازه گیری pH در عصاره اشباع خاک
- درصد اشباع خاک
- درصد اولیه رطوبت خاک
- شناسایی بافت خاک
- تعیین چگالی مواد
- اندازه گیری EC در عصاره اشباع خاک
- اندازه گیری سولفات در عصاره اشباع خاک
- اندازه گیری سدیم در عصاره اشباع خاک
- اندازه گیری پتاسیم در عصاره اشباع خاک
- اندازه گیری منیزیم در عصاره اشباع خاک
-
آنالیزهای صنایع غذایی
- آنالیز چربی (سوکسله)
- اندازه گیری چربی لبنیات با روش ژربر
- آزمون اندازه گیری کربوهیدرات ها در مواد خوراکی
- آزمون بریکس در ۲۰ درجه سلسیوس
- اندازه گیری TVN مقدار ازت فرار
- اندازه گیری پراکسید چربی
- اندازه گیری نمک در مواد غذایی
- اندازه گیری خاکستر مواد غذایی
- اندازه گیری رطوبت در مواد غذایی
- سنجش پروتئین در مواد غذایی
-
آزمایشات میکروبیولوژی مواد غذایی
- آنالیز کپک و مخمر
- شناسایی اشرشیاکلی در مواد غذایی
- شناسایی تخم انگل در میوه و سبزیجات
- تشخیص استافیلوکوک های گواکولاز مثبت به روش MPN
- شمارش اسپور باکتری ها (هوازی و بی هوازی)
- تشخیص سالمونلا در مواد غذایی
- جداسازی باکتری های مزوفیل و ترموفیل
- تشخیص کلی فرم در مواد غذایی
- اندازه گیری فلزات سنگین در مواد غذایی
-
خدمات بخش بیوشیمی و عصاره گیری
-
خدمات بخش بیوشیمی و عصاره گیری
- ارزیابی ظرفیت آنتی اکسیدانی به روش رادیکال DPPH
- خدمات عصاره گیری با سوکسله
- عصاره گیری به روش ماسراسیون یک گیاه
-
- آنالیز سنگ، خاک و مواد معدنی
-
خدمات تحلیل و تفسیر آنالیزها
- تحلیل نتایج و تفسیر آنالیز XRD
- تحلیل و تفسیر نتایج آنالیز FTIR
- تحلیل و تفسیر نتایج آنالیز DRS
- تحلیل و تفسیر نتایج آنالیز BET
- رسم نمودار هیستوگرام و تعیین سایز ذرات TEM/SEM
- تحلیل و تفسیر نتایج میکروسکوپ HR-TEM
- تحلیل و تفسیر نتایج آنالیز XPS
- تحلیل و تفسیر نتایج آنالیز DLS
- تحلیل و تفسیر نتایج آزمون سمیت شناسی MTT
- تحلیل و تفسیر نتایج آنالیز NMR
- خدمات شناسایی انواع مواد
- خدمات آنالیز و فرآوری مواد معدنی
- تعرفه خدمات
- آکادمی مهامکس
- درباره مهامکس
تخفیفهای لبزنت
بررسی مدل و سینتیک رهایش دارو
پس از بدست آمدن نمودار پروفایل رهایش می توان اطلاعات مفید دیگری نیز از نمودار بدست آورد. به عنوان مثال می توان نوع مکانیزم رهایش دارو و سینتیک آن در سامانههای دارورسانی را از طریق معادلات ریاضی تعیین کرد. هدف از مدلسازی ریاضی بیان ساده فرآیند پیچیده رهایش بهمنظور فهم چگونگی سازوکار رهایش در یک سامانه حامل دارو میباشد. به این ترتیب یک مدل ریاضی به طور عمده روی یک یا دو نیروی محرکه اصلی متمرکز میشود. پنج مدل سینتیکی درجه صفر، درجه یک، مدل هیگوچی، هیگسون کراول و کراسمیر پپاس از شناخته شده ترین معادلات می باشند. در مهامکس بررسی مدل رهایش دارو توسط متخصصین برای سامانه های دارورسانی و نتایج بدست آمده از مطالعه رهایش دارو انجام می شود.
مشخصات دستگاه های آماده برای ارائه خدمات بررسی مدل و سینتیک رهایش دارو
درباره آنالیز
بررسی مدل و سینتیک رهایش دارو
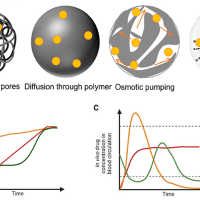
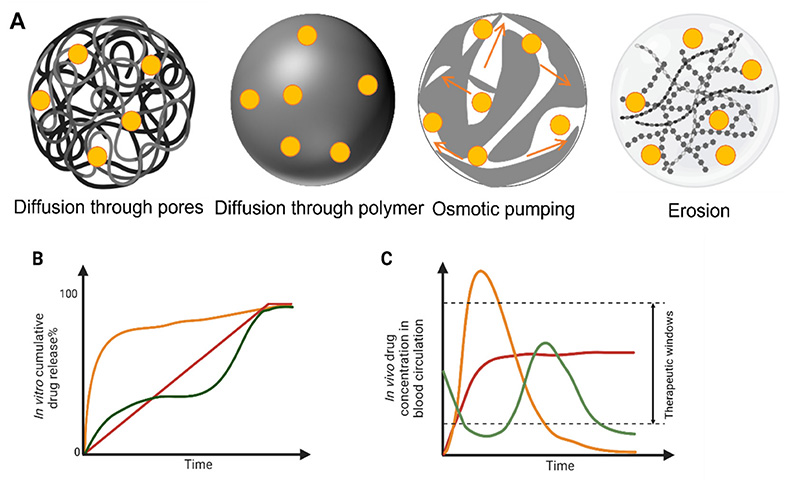
پس از بدست آمدن نمودار پروفایل رهایش می توان اطلاعات مفید دیگری نیز از نمودار بدست آورد. به عنوان مثال تعیین نوع مکانیزم رهایش دارو. سامانههای دارورسانی، داروها را در طی یک دوره زمانی مشخص و بر اساس نیاز درمانی رسانش میکند. رهایش کنترلشده بهمنظور حفظ غلظت مؤثر دارو در بافت هدف یا سلولها یک ویژگی کلیدی این سامانهها است. انواع سامانههای دارورسانی با رهایش دارویی کنترلشده را میتوان بهصورت زیر دسته بندی کرد:
۱- سامانههایی که سرعت رهایش دارو از طریق انحلال دارو کنترل میشود.
۲- سامانههایی که سرعت رهایش دارو از طریق پدیده نفوذ دارو کنترل میشود.
۳- سامانههایی که سرعت رهایش دارو از طریق انحلال و نفوذ دارو کنترل میشود.
۴- سامانههایی که سرعت رهایش دارو از طریق رسوخ آب به سامانه کنترل میشود.
۵- سامانههایی که سرعت رهایش دارو از طریق شیمیایی کنترل میشود.
۶- هیدروژل ها
۷- رزینهای تبادل یونی
پتانسیلهای فرمولاسیونهایی با قابلیت آزادسازی کنترلشده دارو، داروسازها و مهندسین را بهمنظور درک بیشتر مکانیزم های رهایش دارو بهمنظور طراحی هر چه بهتر سامانههای دارورسانی در کنار هم قرار داده است. برای رسیدن به این هدف، استفاده از مدلهای ریاضی میتواند بسیار مؤثر بوده و سینتیکهای آزادسازی را پیش بینی کند. هدف از مدلسازی ریاضی بیان ساده فرآیند پیچیده رهایش بهمنظور فهم چگونگی سازوکار رهایش در یک سامانه حامل دارو میباشد. به این ترتیب یک مدل ریاضی به طور عمده روی یک یا دو نیروی محرکه اصلی متمرکز میشود. البته این مدلها ممکن است برای تشریح بعضی از سامانههای انتقالی پیچیدهتر کافی نباشند.
بهمنظور مطالعه سینتیک رهایش یک دارو، نتایج بدست آمده را می توان با پنج مدل سینتیکی درجه صفر، درجه یک، مدل هیگوچی، هیگسون کراول و کراسمیر پپاس توسط نرم افزار MATLAB برازش کرد. مدلهای مورد مطالعه به شرح زیر میباشند:
- مدل درجه صفر Qt = Q0 + K0t
در مدل درجه صفر، مقدار داروی حل شده، غیر وابسته به میزان اولیه دارو است. در این رابطه Qt مقدار داروی حل شده تا زمان t، K0 ثابت رهایش درجه صفر و Q0 مقدار اولیه دارو در محلول بافری است که در مورد مطالعه فوق برابر با صفر است.
- مدل درجه یک Ln Mt = Ln M0 + K1t
در این مدل تغییرات مقدار حل نشده از دارو به زمان، با توان اول مقدار داروی حل نشده ارتباط مستقیم دارد. در این رابطه Mt مقدار داروی حل نشده در زمان t، M0 مقدار اولیه دارو و K1 ثابت رهایش درجه اول میباشد.
- مدل هیگوچی Qt = kHt 1/2
در این رابطه رهایش دارو به وسیله نفوذ مواد محلول از حامل کنترل میشود و مکانیزم آزادسازی از نفوذ پیروی میکند. در این مدل مقدار دارو حل شده با ریشه دوم زمان در ارتباط است. Qt مقدار دارو حل شده در زمان t و KH ثابت انحلال هیگوچی است. این مدل بر اساس این قضیه پایگذاری شده است که نفوذ تنها در یک بعد اتفاق می افتد، ابعاد ذرات بسیار کوچکتر از سیستم است و پدیده تورم و حل شدن پلیمر قابل صرف نظر کردن است.
- مدل هیگسون – کراول Q0 1/3 – Qt 1/3 = KHCt
Qt در این رابطه مقدار دارو رها شده در زمان t، Q0 مقدار اولیه دارو در ذرات تولیدی و KHC ثابت سرعت برای معادله هیگسیون - کراول است.
- مدل کراسمیر – پپاس Mt/M∞ = ktn
Mt/M نسبت داروی رها شده از سیستم در زمان t است. میزان n نشان دهنده مکانیزم رهایش دارو است. اگرچه این میزان به ساختار هندسی سیستم نیز بستگی دارد، با این حال بهصورت حدودی اگر n معادل 5/0 باشد، مکانیزم رهایش از قانون فیک یا پدیده نفوذ پیروی میکند. اگر مقدار n بین 5/0 تا یک باشد مکانیزم نفوذ و فرسایش ماتریکس حامل در رهایش دارو مؤثر است و اگر n برابر یک باشد، رهایش دارو مستقل از زمان است و یا به عبارتی از مدل درجه صفر پیروی میکند. در سایر حالات مکانیزم خاصی را نمیتوان برای رهایش دارو عنوان نمود. مقدار n برای سیستمهای دارویی کروی نزدیک به 43/0 است.
جهت اطلاعات تکمیلی به مقاله می توانید مراجعه کنید:
Ghaffari, S.B., Sarrafzadeh, M.H., Fakhroueian, Z. and Khorramizadeh, M.R., 2019. Flower-like curcumin-loaded folic acid-conjugated ZnO-MPA-βcyclodextrin nanostructures enhanced anticancer activity and cellular uptake of curcumin in breast cancer cells. Materials Science and Engineering: C, 103, p.109827.